過去一個(gè)月，AI在多個(gè)領(lǐng)域出現(xiàn)了巨大的飛躍。
賓夕法尼亞大學(xué)沃頓商學(xué)院教授Ethan Mollick在近日一篇文章中，總結(jié)了他所觀察到的人工智能最新進(jìn)展，以及這些進(jìn)展的含義。Mollick的專業(yè)是研究創(chuàng)業(yè)與創(chuàng)新以及人工智能，并致力于探索人工智能對(duì)工作和教育的意義。
Mollick觀察到，人工智能在近一個(gè)月發(fā)生了突破性的進(jìn)展：
（1）在以GPT-4為代表的智能人工智能已經(jīng)無(wú)處不在的情況下，更聰明的人工智能正在出現(xiàn)，尤其是Gen3和o1模型的發(fā)布；
（2）隨著視覺功能的引入，ChatGPT 和 Gemini 現(xiàn)在都可以同時(shí)觀看實(shí)時(shí)視頻和語(yǔ)音交互。能夠通過最常見的人類感官（視覺和聲音）與人類實(shí)時(shí)互動(dòng)的模型將 AI 變成與您同在房間里的陪伴者，而不是被困在計(jì)算機(jī)上聊天框中的實(shí)體；
（3）AI 視頻突然變得非常好，但真正的飛躍來(lái)自上周出現(xiàn)的人工智能文本轉(zhuǎn)視頻生成器。
Mollick表示，我們還遠(yuǎn)遠(yuǎn)沒有看到人工智能進(jìn)步的終結(jié)，引人注目的不僅僅是個(gè)別的突破，而是變革的速度和廣度。人工智能正以以不均勻的速度大幅跨越，甚至超出了人類能輕松衡量其影響的能力。
以下為Mollick文章全文翻譯：
上個(gè)月，人工智能的狀況發(fā)生了變化，僅在上周，變化速度就急劇加快。人工智能實(shí)驗(yàn)室推出了大量新產(chǎn)品，有些是革命性的，有些是漸進(jìn)式的，讓人難以跟上。我相信，這些變化中有幾個(gè)是真正的突破，將重塑人工智能（也許還有我們的）的未來(lái)。以下是我們的現(xiàn)狀：
人工智能如今無(wú)處不在
去年年底，只有一個(gè)公開可用的 GPT-4/ Gen2類模型，那就是 GPT-4。現(xiàn)在有六到十個(gè)這樣的模型，其中一些是開源的，這意味著任何人都可以免費(fèi)使用或修改它們。來(lái)自美國(guó)的有 OpenAI 的 GPT-4o、Anthropic 的 Claude Sonnet 3.5、谷歌的 Gemini 1.5、Meta 的開放 Llama 3.2、埃隆·馬斯克的 Grok 2 和亞馬遜的新 Nova。中國(guó)公司已經(jīng)發(fā)布了三種似乎具有 GPT-4 級(jí)性能的開放多語(yǔ)言模型，尤其是阿里巴巴的 Qwen、R1 的 DeepSeek 和 01.ai 的 Yi。歐洲在這個(gè)領(lǐng)域只有一家參與者，那就是法國(guó)的 Mistral。這一堆令人困惑的名字意味著，構(gòu)建有能力的人工智能并非只涉及 OpenAI 獨(dú)有的神奇公式，而是任何擁有計(jì)算機(jī)科學(xué)人才以及能夠獲得訓(xùn)練模型所需的芯片和算力的公司都能夠做到。
事實(shí)上，GPT-4 級(jí)別的人工智能在發(fā)布時(shí)令人震驚，引發(fā)了人們對(duì)未來(lái)的極大擔(dān)憂，而現(xiàn)在它可以在我的家用電腦上運(yùn)行了。Meta 本月發(fā)布的最新小型型號(hào)名為L(zhǎng)lama 3.3 ，它提供了類似的性能，并且可以在我的游戲電腦上完全離線運(yùn)行。微軟新推出的微型Phi 4是 GPT-4 級(jí)別的，幾乎可以在手機(jī)上運(yùn)行，而其性能稍差的前代產(chǎn)品 Phi 3.5 更是可以。某種程度上的智能是按需提供的。
我家用電腦上運(yùn)行的 Llama 3.3 通過了“涉及奶酪雙關(guān)語(yǔ)的押韻詩(shī)”基準(zhǔn)測(cè)試，只有幾個(gè)不自然的雙關(guān)語(yǔ)。
而且，正如我所討論過的（很快會(huì)再次發(fā)布），這些無(wú)處不在的人工智能現(xiàn)在開始為代理提供動(dòng)力，這些代理是可以追求自己目標(biāo)的自主人工智能。你可以在我之前的文章中看到這意味著什么，我使用早期的代理進(jìn)行購(gòu)物比較和監(jiān)控建筑工地。
非常聰明的人工智能現(xiàn)在已經(jīng)出現(xiàn)
所有這些意味著，如果 GPT-4 級(jí)別的性能是 AI 可以達(dá)到的最高水平，那么隨著我們逐漸習(xí)慣它們的能力，這可能足以讓我們經(jīng)歷五到十年的持續(xù)變化。但沒有跡象表明 AI 發(fā)展即將大幅放緩。我們之所以知道這一點(diǎn)，是因?yàn)樯蟼€(gè)月還有另外兩個(gè)重要的發(fā)布——Gen3 模型的首次發(fā)布（你可以將它們視為 GPT-5 類模型）和 o1 模型的發(fā)布，這些模型可以在回答之前“思考”，這實(shí)際上使它們比其他 LLM 的推理能力強(qiáng)得多。我們正處于 Gen3 發(fā)布的早期階段，所以我不會(huì)在這篇文章中過多地介紹它們，但我確實(shí)想談?wù)?o1。
當(dāng) o1 以早期的 o1-preview 形式發(fā)布時(shí)，我曾討論過它，但兩個(gè)更復(fù)雜的版本 o1 和 o1-pro 的功能顯著增強(qiáng)。這些模型在回答問題之前會(huì)花時(shí)間進(jìn)行隱形“思考”——模仿人類的邏輯問題解決方式。這種方法稱為測(cè)試時(shí)間計(jì)算，事實(shí)證明，它是讓模型更好地解決問題的關(guān)鍵。事實(shí)上，這些模型現(xiàn)在已經(jīng)足夠聰明，能夠以大大小小的方式為研究做出有意義的貢獻(xiàn)。
舉一個(gè)有趣的例子，我讀到一篇關(guān)于最近社交媒體恐慌的文章——一篇學(xué)術(shù)論文指出，黑色塑料餐具可能會(huì)毒害人類，因?yàn)樗鼈儾糠质怯苫厥盏碾娮永瞥傻摹Ｔ撜撐闹赋觯环N名為 BDE-209 的化合物從這些餐具中滲出的速率非常高，接近美國(guó)環(huán)保署設(shè)定的安全劑量水平。很多人都扔掉了他們的鍋鏟，但麥吉爾大學(xué)的 Joe Schwarcz 認(rèn)為這沒有道理，并發(fā)現(xiàn)了一個(gè)數(shù)學(xué)錯(cuò)誤，作者在文章的第七頁(yè)錯(cuò)誤地將 BDE-209 的劑量乘以了 10 倍——這個(gè)錯(cuò)誤被論文作者和同行評(píng)審員忽略了。我很好奇 o1 是否能發(fā)現(xiàn)這個(gè)錯(cuò)誤。因此，我從手機(jī)上粘貼了PDF 文本并輸入：“仔細(xì)檢查本文中的數(shù)學(xué)計(jì)算”。就這樣。o1 立即發(fā)現(xiàn)了錯(cuò)誤（其他 AI 模型沒有）。
當(dāng)模型不僅能夠處理整篇學(xué)術(shù)論文，還能理解“檢查數(shù)學(xué)”的意義所在，然后成功檢查結(jié)果時(shí)，人工智能的能力就會(huì)發(fā)生根本性的變化。事實(shí)上，我的實(shí)驗(yàn)以及其他人的實(shí)驗(yàn)都激發(fā)了人們?nèi)パ芯?o1 能在科學(xué)文獻(xiàn)中發(fā)現(xiàn)錯(cuò)誤的頻率。我們不知道 o1 能多頻繁地完成這種壯舉，但找出答案似乎很重要，因?yàn)樗赶蛄四芰Φ男虑把亍?/section>
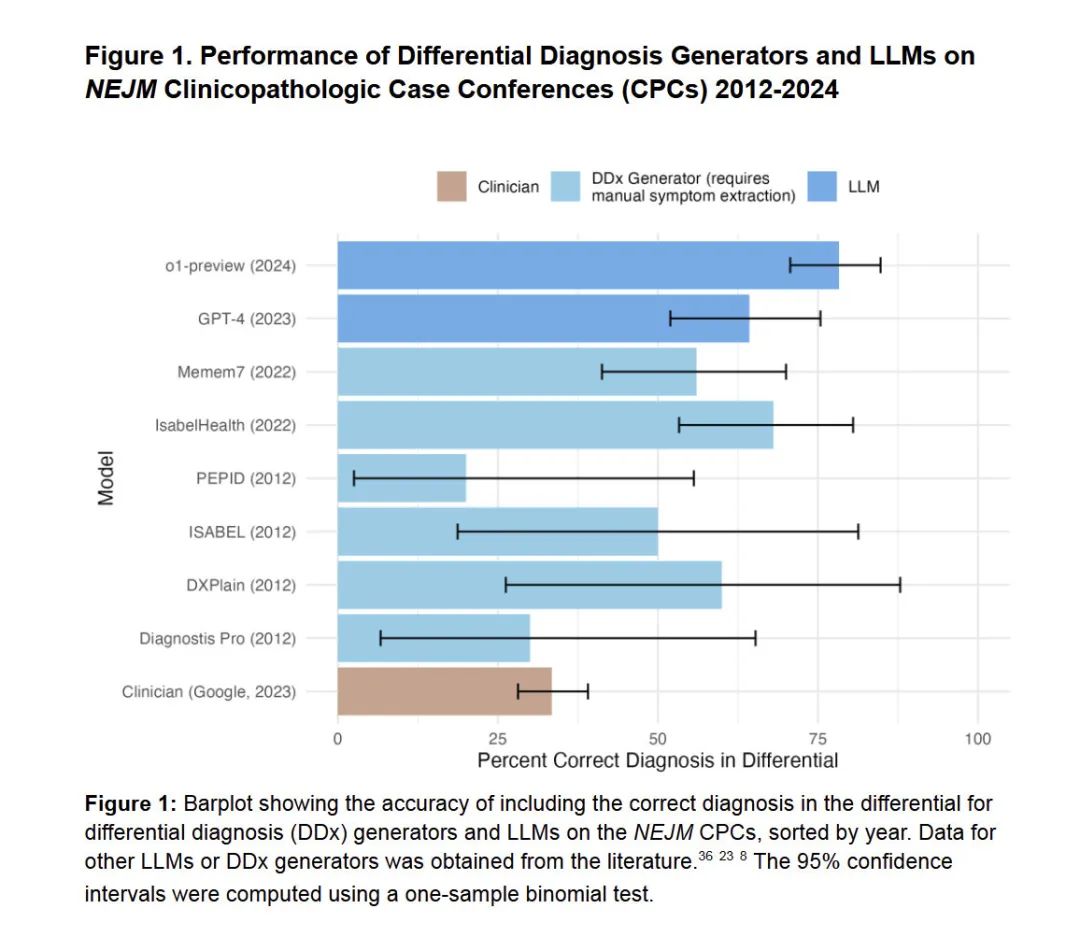
事實(shí)上，即使是 o1 的早期版本，即預(yù)覽模型，似乎也代表了科學(xué)能力的飛躍。哈佛大學(xué)、斯坦福大學(xué)和其他研究人員發(fā)表了一篇令人震驚的醫(yī)學(xué)工作論文，結(jié)論是“o1-preview 在鑒別診斷、診斷臨床推理和管理推理方面表現(xiàn)出超人的表現(xiàn)，在多個(gè)領(lǐng)域都優(yōu)于前幾代模型和人類醫(yī)生。”這篇論文還沒有經(jīng)過同行評(píng)審，它并沒有表明人工智能可以取代醫(yī)生，但它和上面的結(jié)果確實(shí)表明，這個(gè)世界正在發(fā)生變化，不把人工智能作為第二意見可能很快就會(huì)成為一個(gè)錯(cuò)誤。
可能更重要的是，越來(lái)越多的研究人員告訴我，o1，尤其是 o1-pro，正在產(chǎn)生新穎的想法并解決他們領(lǐng)域中意想不到的問題。問題是，現(xiàn)在只有專家才能評(píng)估人工智能是錯(cuò)還是對(duì)。例如，我非常聰明的沃頓商學(xué)院同事Daniel Rock讓我給 o1-pro 一個(gè)挑戰(zhàn)：“讓它使用文獻(xiàn)中沒有的證明來(lái)證明神經(jīng)網(wǎng)絡(luò)的通用函數(shù)逼近定理，而無(wú)需 1）假設(shè)無(wú)限寬的層和 2）超過 2 層。” 以下是它回復(fù)的內(nèi)容：
